Logistics 模型
1 算法介绍
logistics 方程由比利时数学家Pierre François Verhulst提出,是一个对S型曲线进行数学描述的模型。这个方程应用于一些特殊的领域建模与预测,例如单位面积内某种生物的数量、人口数量等社会经济指标、某种商品(例如手机)的普及率等。
2 原理
logistics 方程定义:
\[x_t = \frac{1}{c+ae^{bt}} \tag{1}\]其中,t 表示时间变量,a,b,c 为模型的参数;当趋势比较完整时, $a>0, b<0, c>0$ 。其曲线如下图:
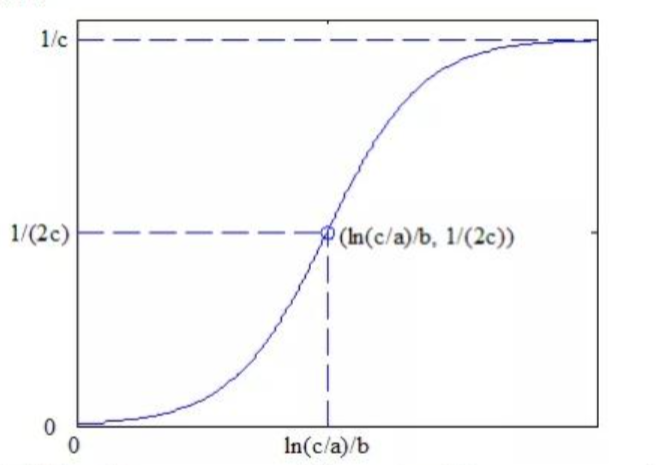
根据方程和图像可知:
当 $t \to -\infty,x(t) \to 1/c $。为研究 Logistics 曲线好的增长特性,对 Logistics 方程求一阶导数:
\[\frac{dx}{dt}=\frac{-abe^{bt}}\{\{(c+a e^{bt})}^2} > 0\]2.1 Yule 算法
根据方程 (1),微分写成差分式:
$ \frac{x_{t+1}-x_t}{x_{t+1}} $
$ = 1 - \frac{x_t}{x_{t+1}} $
$ = 1 - \frac{c+ae^{b(t+1)}}{c+ae^{bt}} $
$ = \frac{(ae^{bt}+c-c)(1-e^b)}{c+ae^{bt}} $
$ = (1-e^b)-c(1-e^b)x_t $
设 $z_t=\frac{x_{t+1}-x_t}{x_{t+1}}, \gamma=1-e^b, \beta=-c(1-e^b)$,那么上面的方程可以写成线性方程:
\[z_t=\gamma+\beta x_t\]利用最小二乘法(OLS)可以得到这个方程参数的估计值,进而 b 和 c 的估计值也可以进一步得到。
为了得到 a 的估计值,Logistics 方程两边同时取对数:
\[ln(\frac{1}{x_t}-\hat{c})=ln \hat{a}+\hat{b}t \tag{2}\]左右分别对 t 求和:
\[\sum_{t=1}^{n} ln(\frac{1}{x_t}-\hat{c})=nln\hat{a}-\frac{n(n+1)}{2}\hat{b} \tag{3}\]可以很容易得到 a 的估计值:
\[\hat{a}=exp \left( \frac{1}{n} \left( \sum_{t=1}^n ln(\frac{1}{x_t}-\hat{c}-\frac{n(n+1)}{2}\hat{b}) \right) \right) \tag{4}\]2.2 Rhodes 算法
根据 Logistics 方程可以得到:
$ \frac{1}{x_{t+1}} $
$ = c + ae^{b(t+1)} $
$ =c-ce^b+ce^b+ae^{b(t+1)} $
$ =c(1-e^b)+\frac{e^b}{x_t} $
设 $z_t=\frac{1}{x_{t+1}}、s_t=\frac{1}{x_t}、\gamma =c(1-e^b)、\beta =e^b$,那么该方程可以写成线性方程:
\[z_t=\gamma + \beta s_t\]利用最小二乘法(OLS)可以得到这个方程参数的估计值,进而 b 和 c 的估计值也可以进一步得到。利用方程 (2)-(4) 可以得到 a 的估计值。
2.3 Nair 算法
Yule 算法的差分式结果可以进一步写成:
$\frac{x_{t+1}-x_t}{x_{t+1}}=(1-e^b)(1-cx_t)$ $\frac{1}{1-e^b}=\frac{x_{t+1}(1-cx_t)}{x_{t+1}-x_t}$ $\frac{1+e^b}{1-e^b}=\frac{2}{1-e^b}-1$ $=\frac{\frac{1}{x_t}+\frac{1}{x_{t+1}}-2c}{\frac{1}{x_t}-\frac{1}{x_{t+1}}}$
进一步整理得到;
\[\frac{1}{x_t}-\frac{1}{x_{t+1}} = \frac{1-e^b}{1+e^b}(\frac{1}{x_t}+\frac{1}{x_{t+1}})-\frac{2c(1-e^b)}{1+e^b} \tag{5}\]设 $z_t=\frac{1}{x_t}-\frac{1}{x_{t+1}}、s_t=\frac{1}{x_t}+\frac{1}{x_{t+1}}、\gamma =\frac{2c(1-e^b)}{1+e^b}、\beta = \frac{1-e^b}{1+e^b}$ ,那么方程 (5) 可以写成线性方程:
\[z_t = \gamma + \beta s_t\]利用最小二乘法(OLS)可以得到这个方程的参数估计值,进而 b 和 c 的估计值也可以得到,利用方程 (2)-(4) 可以得到 a 的估计值。
3 Logistics 模型与 Logistics 回归理解与使用
Logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。Logistic回归的因变量可以是二分类的,也可以是多分类的。
3.1 Logistic回归跟多元线性回归差不多,但是有区别
- 线性回归:y是一个定量的变量,这时y对于不同的自变量来说有相应的值。
- Logistic回归:y是一个定性的变量,比如y只能等于0或1。
3.2 模型的基本形式
\[P(Y=1 | x_1, x_2, ..., x_n)=\frac{exp(\beta _0+\beta _1x_1 + ... + \beta _n x_n)}{1+exp(\beta _0+\beta _1x_1 + ... + \beta _n x_n)}\]在实际应用该模型的时候,常常不是不是直接对P进行回归,而是先 定义单调连续概率函数 $\pi$ :
\[\pi=P(Y=1 | x_1, x_2, ..., x_n), 0 < \pi < 1\]于是Logistic模型就可以变形为:
\[ln\frac{\pi}{1- \pi}=\beta _0+\beta _1x_1 + ... + \beta _n x_n, 0 < \pi < 1\]即:
\[ln\frac{\pi}{1- \pi}=\beta _0+\beta _1x_1 + ... + \beta _n x_n, 0 < \pi < 1 \tag{1}\] \[\pi=\frac{exp(\beta _0+\beta _1x_1 + ... + \beta _n x_n)}{1+exp(\beta _0+\beta _1x_1 + ... + \beta _n x_n)} \tag{2}\] \[P=\begin{cases} 0 & \pi \le A \\ 1 & \pi \ge 1 - A \end{cases} \tag{3}\]通过多元线性回归解出 $\beta _0, \beta _1, …, \beta _n$ ,带入求得 $\pi$ ,根据 $\pi$ 的值判断 P 的取值。